#约束系统概述

在传统上，计算机程序总被组织成一种单向的计算，它们对一些事先给定的参数执行某些操作，产生出所需要的输出。但在另一方面，我们也经常需要模拟一些由各种量之间的关系描述的系统。例如，某个机械结构的数学模型里可能包含着这样的一些信息：在一个金属杆的偏转量d与作用于这个杆的力F、杆的长度L、截面面积A和弹性模数之间的关系可以由下面方程描述：

dAE = FL

这种关系并不是单向的，给定了其中任意的4个量，我们就可以利用它们计算出第5个变量。然而，要将这种方程翻译到传统的程序设计语言，就会迫使我们选出一个量，要求基于另外的4个量去计算它。这样，一个用于计算面积A的过程将不能用于计算偏转量d，虽然对于A和d的计算都来自这同一个方程。

我们需要描绘一种语言的设计，这种语言将使我们可以基于各种关系进行工作。这一语言的基本元素就是基本约束。它们描述了在不同量之间的某种特定关系。例如(adder a b c)描述的是量a、b和c必须有关系a + b = c，(multiplier x y z)描述的是约束关系xy = z，而(constant 3.14 x)表示的是x的值永远都是3.14。在这里，我们通过构造约束网络的方式组合各种约束，在这样的约束网络里，约束通过连接器连接起来。连接器也是一种对象，它们保存一个值，使之能参与一个或者多个约束。例如，我们知道在华氏温度和摄氏温度之间的关系是：

9C = 5(F - 32)

这样的约束就可以看做是一个网络

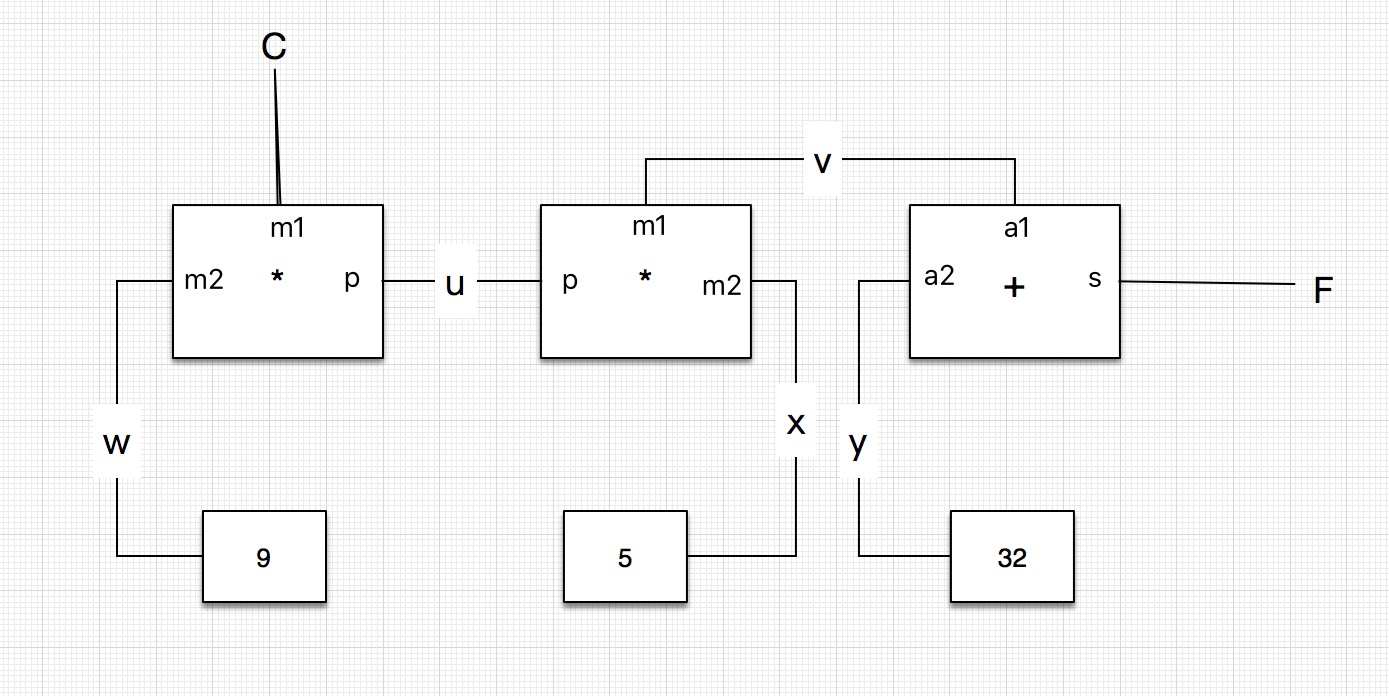
通过基本的加法约束、乘法约束和常量约束组成。在这个图里，我们看到左边的乘法块有三个引线，分别标记为m1、m2和p。该乘法约束的这些引线以如下方式连接到网络的其他部分：引线m1连到连接器C，这个连接器将保存摄氏温度。引线m2接在连接器w，该连接器还连接着一个保存常量9的约束块。引线p被这一乘法块约束到m1和m2的乘积，它还连接到另一个乘法块的引线p。另一个乘法块的m2连接到常量5，它的m1连接到另一个加法快的一条引线上。

由这样的网络完成的计算以如下方式进行：当某个连接器被给定了一个值时（由用户或者由它所连接的某个约束块），它就会去唤醒所有与之关联的约束（除了刚刚唤醒它的那个约束之外）。通知它们自己有了一个新值。被唤醒的每个约束块将去盘点自己的连接器，看看是否存在足够的信息为某个连接器确定一个值。如果可能的话，该块就设置相应的连接器，而这个连接器又会去唤醒与之连接的约束，并这样进行下去。

#约束系统的使用

针对上面的约束网络图，我们得到以下代码：

    Connector *C = new Connector();
    Connector *F = new Connector();

    Connector *u = new Connector();
    Connector *v = new Connector();
    Connector *w = new Connector();
    Connector *x = new Connector();
    Connector *y = new Connector();

    Constraint *mul1 = new Multiplier(C, w, u, "mul1");
    Constraint *mul2 = new Multiplier(v, x, u, "mul2");
    Constraint *adder = new Adder(v, y, F, "add1");

    Constraint *con1 = new Constant(w, 9, "con1");
    Constraint *con2 = new Constant(x, 5, "con2");
    Constraint *con3 = new Constant(y, 32, "con3");

    C->setValue(10, "shenao");
    cout << F->getValue() << endl;

    //在设置新的值前，先用忘掉之前的旧值
    C->forgetValue("shenao");
    F->setValue(200, "shenao");
    cout << C->getValue() << endl;